如图,平面直角坐标系中有一直角梯形OMNH,点H的坐标为(-8,0),点N的坐标为(-6,-4).
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A, 点N的对应点为B, 点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若 ,求EF和半径OA的长.

为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A种树苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.

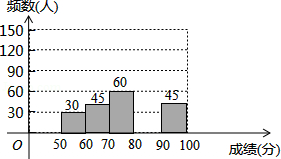
为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
|
组别 |
分数段 |
频数(人) |
频率 |
|
1 |
50≤x<60 |
30 |
0.1 |
|
2 |
60≤x<70 |
45 |
0.15 |
|
3 |
70≤x<80 |
60 |
n |
|
4 |
80≤x<90 |
m |
0.4 |
|
5 |
90≤x<100 |
45 |
0.15 |
请根据以图表信息,解答下列问题:
(1)表中m= ,n= ;
(2)补全频数分布直方图;
(3)全体参赛选手成绩的中位数落在第几组;
(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.
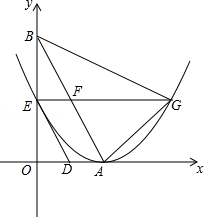
如图,直线 与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和 个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
(1)求点A,点B的坐标;
(2)用含t的代数式分别表示EF和AF的长;
(3)当四边形ADEF为菱形时,试判断△AFG与△AGB是否相似,并说明理由.
(4)是否存在t的值,使△AGF为直角三角形?若存在,求出这时抛物线的解析式;若不存在,请说明理由.