(本小题满分12分)已知数列{an}中,a1=2,前n项和为Sn,对于任意n≥2,
3Sn-4,an, 总成等差数列.
总成等差数列.
(I)求数列 通项公式an;
通项公式an;
(II)若数列 满足
满足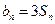 ,求数列
,求数列 的前n项和
的前n项和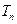 .
.
已知幂函数f(x)=x(m2+m)-1(m∈N*),经过点(2,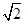 ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
函数f(x)=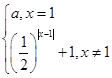 ,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.
,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.
已知函数f(x)=2x,x∈R.当m取何值时方程|f(x)-2|=m有一个解?两个解?
已知函数f(x)=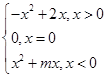 是奇函数.
是奇函数.
(1)求实数m的值;
(2)若函数f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围.
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),
当0≤x≤1时,f(x)=x.
(1)求f(3)的值;
(2)当-4≤x≤4时,求f(x)的图像与x轴所围成图形的面积.