(本小题满分12分)
已知直线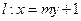 过椭圆
过椭圆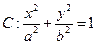 的右焦点
的右焦点 ,抛物线:
,抛物线: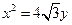 的焦点为椭圆
的焦点为椭圆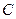 的上顶点,且直线
的上顶点,且直线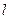 交椭圆
交椭圆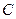 于
于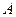 、
、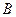 两点,点
两点,点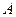 、
、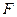 、
、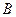 在直线
在直线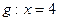 上的射影依次为点
上的射影依次为点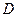 、
、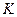 、
、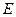 .
.
(1)求椭圆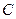 的方程;
的方程;
(2)若直线l交y轴于点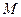 ,且
,且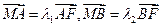 ,当
,当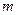 变化时,探求
变化时,探求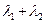 的值是否为定值?若是,求出
的值是否为定值?若是,求出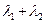 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接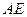 、
、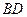 ,试探索当
,试探索当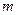 变化时,直线
变化时,直线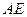 与
与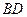 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
(本小题满分12分)已知向量 的夹角为
的夹角为 .
.
(1)求 ;(2)若
;(2)若 ,求
,求 的值.
的值.
(本小题满分12分)函数f(x)=3sin 的部分图像如图所示.
的部分图像如图所示.
(1)写出f(x)的最小正周期及图中x0,y0的值;
(2)求f(x)在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)设向量a=(4cosα,sinα),b=(sinβ,4cosβ),c=(cosβ,-4sinβ),
(1)若a与b-2c垂直,求tan(α+β)的值;
(2)求|b+c|的最大值.
(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为( ,
, ),记∠COA=α.
),记∠COA=α.
(Ⅰ)求 的值;
的值;
(Ⅱ)求cos∠COB的值.
(本小题满分10分)已知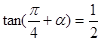 .
.
(Ⅰ)求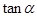 的值;
的值;
(Ⅱ)求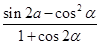 的值.
的值.