某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.若每日来回的次数是车头每次拖挂车厢节数的一次函数,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图,在直观图中, 是
是 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)求出该几何体的体积;
(2)若 是
是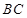 的中点,求证:
的中点,求证: ∥平面
∥平面 ;
;
(3)求证:平面 ⊥平面
⊥平面 .
.
如图,在直角梯形 中,
中,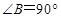 ,
,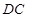 ∥
∥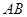 ,
, ,
,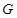 为线段
为线段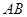 的中点,将
的中点,将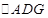 沿
沿 折起,使平面
折起,使平面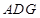 ⊥平面
⊥平面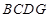 ,得到几何体
,得到几何体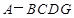 .
.
(1)若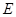 ,
, 分别为线段
分别为线段 ,
, 的中点,求证:
的中点,求证: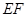 ∥平面
∥平面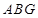 ;
;
(2)求证: ⊥平面
⊥平面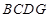 ;
;
(3)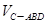 的值.
的值.
设函数f(x)=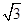 cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为 .
.
(1)求ω的值;
(2)如果f(x)在区间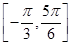 上的最小值为
上的最小值为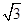 ,求a的值.
,求a的值.
已知向量m=(sinA,cosA),n=(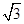 ,-1),m·n=1,且A为锐角.
,-1),m·n=1,且A为锐角.
(1)求角A的大小;
(2)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
已知某海滨浴场的海浪高达y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据.
| t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
| y(米) |
1.5 |
1.0 |
0.5 |
1.0 |
1.5 |
1.0 |
0.5 |
0.99 |
1.5 |
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多长时间可供冲浪者进行运动?