如图,在直角梯形 中,
中,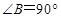 ,
,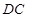 ∥
∥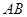 ,
, ,
,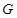 为线段
为线段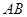 的中点,将
的中点,将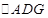 沿
沿 折起,使平面
折起,使平面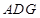 ⊥平面
⊥平面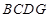 ,得到几何体
,得到几何体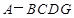 .
.
(1)若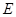 ,
, 分别为线段
分别为线段 ,
, 的中点,求证:
的中点,求证: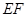 ∥平面
∥平面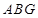 ;
;
(2)求证: ⊥平面
⊥平面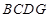 ;
;
(3)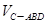 的值.
的值.
已知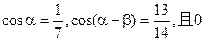 <
<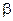 <
< <
<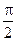 ,
,
(Ⅰ)求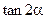 的值.(Ⅱ)求
的值.(Ⅱ)求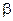 .
.
如图,在长方体ABCD—A1B1C1D1中,AB= AD=2.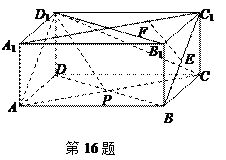
(1)证明:面BDD1 B1⊥面ACD1;
(2)若E是BC1的中点,P是AC的中点,F是A1C1上的点, C1F=mFA1,试求m的值,使得EF∥D1P.
(本小题满分14分)
某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:
| 序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 身高x(厘米) |
192 |
164 |
172 |
177 |
176 |
159 |
171 |
166 |
182 |
166 |
| 脚长y( 码 ) |
48 |
38 |
40 |
43 |
44 |
37 |
40 |
39 |
46 |
39 |
| 序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 身高x(厘米) |
169 |
178 |
167 |
174 |
168 |
179 |
165 |
170 |
162 |
170 |
| 脚长y( 码 ) |
43 |
41 |
40 |
43 |
40 |
44 |
38 |
42 |
39 |
41 |
(Ⅰ)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的 联列表:
联列表:
| 高个 |
非高个 |
合计 |
|
| 大脚 |
|||
| 非大脚 |
12 |
||
| 合计 |
20 |
(Ⅱ)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:
①抽到12号的概率;②抽到“无效序号(超过20号)”的概率.
已知集合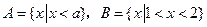 ,且
,且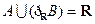 ,则实数
,则实数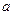 的取值范围
的取值范围
给出定义:若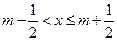 (其中
(其中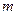 为整数),则
为整数),则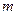 叫做离实数
叫做离实数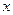 最近的整数,记作
最近的整数,记作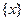 ,即
,即 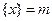 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数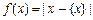 的四个命题:
的四个命题: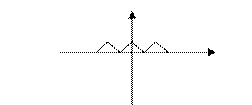
①函数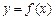 的定义域是R,值域是[0,
的定义域是R,值域是[0,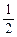 ];
];
②函数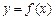 的图像关于直线
的图像关于直线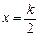 (k∈Z)对称;
(k∈Z)对称;
③函数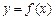 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④函数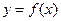 在
在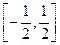 上是增函数;
上是增函数;
则其中真命题是__