给出定义：若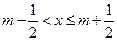
（其中
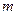为整数），则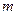叫做离实数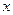
最近的整数，记作
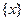，即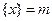 
. 在此基础上给出下列关于函数
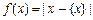的四个命题：
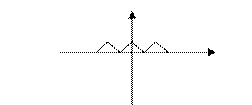
①函数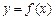
的定义域是R，值域是[0，
]；
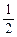②函数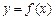的图像关于直线
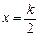(k∈Z)对称；
③函数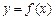是周期函数，最小正周期是1；
④函数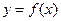
在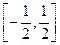
上是增函数；
则其中真命题是__
（本小题满分12分）
已知两点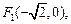
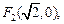满足条件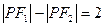
的动点P的轨迹是曲线E，直线l：y= kx－1与曲线E交于A、B两个不同点。
（1）求k的取值范围；（2）如果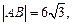
求直线l的方程.
（本小题满分12分）
已知A、B两点的坐标分别是（-1，0）、（1，0），直线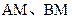
相交于点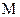
，且它们的斜率之积为
，求点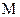的轨迹方程并判断轨迹形状。
（本小题满分12分）
求适合下列条件的圆锥曲线方程:
(1).长轴长是短轴长的3倍,经过点(3,0)的椭圆标准方程。
(2).已知双曲线两个焦点的坐标为
,双曲线上一点P到两焦点的距离之差的绝对值等于6，求双曲线标准方程.
(3).已知抛物线的顶点在原点,准线与其平行线x=2的距离为3,求抛物线标准方程.
（本小题满分12分）
已知命题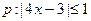
，命题
，若
是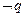
的必要不充分条件，求实数
的取值范围。
已知函数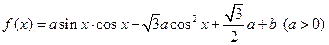
(1)写出函数的单调递减区间；
(2)设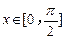
，
的最小值是
，最大值是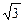
，求实数
的值．