已知函数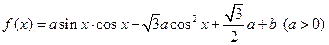
(1)写出函数的单调递减区间;
(2)设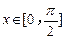 ,
, 的最小值是
的最小值是 ,最大值是
,最大值是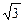 ,求实数
,求实数 的值.
的值.
从某居民区随机抽取10个家庭,获得第 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得 ,
, ,
, ,
, .
.
(Ⅰ)求家庭的月储蓄 对月收入
对月收入 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程 中,
中, ,
, ,
,
其中 ,
, 为样本平均值.
为样本平均值.
如图①,在边长为1的等边
 中,
中, 分别是
分别是 边上的点,
边上的点, ,
, 是
是 的中点,
的中点, 与
与 交于点
交于点 ,将
,将 沿
沿 折起,得到如图②所示的三棱锥
折起,得到如图②所示的三棱锥 ,其中
,其中 .
.
(1) 证明: //平面
//平面 ;
;
(2) 证明:
 平面
平面 ;
;
(3) 当 时,求三棱锥
时,求三棱锥 的体积
的体积 .
.
有一个容量为100的某校毕业生起始月薪的样本数据的分组及各组的频数如下:
| 起始月薪(百元) |
[13,14) |
[14,15) |
[15,16) |
[16,17) |
[17,18) |
[18,19) |
[19,20) |
[20,21] |
| 频数 |
7 |
11 |
26 |
23 |
15 |
8 |
4 |
6 |
(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率分布折线图;
(3)根据频率分布估计该校毕业生起始月薪低于2000元的频率.
正项数列{an}满足 .
.
(1)求数列{an}的通项公式an;
(2)令 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
在△ 中,内角
中,内角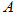 、
、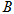 、
、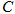 的对边分别是
的对边分别是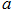 、
、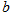 、
、 ,且
,且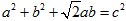 .
.
(Ⅰ)求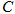 ;
;
(Ⅱ)设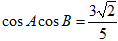 ,
, ,求
,求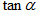 的值.
的值.