如图1，在平面直角坐标系中，拋物线y=ax2+c与x轴正半轴交于点F(16，0)、与y轴正半轴交于点E(0，16)，边长为16的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合；
(1) 求拋物线的函数表达式；
(2) 如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时，点P不与A、B两点重合，点Q不与C、D两点重合)。设点A的坐标为(m，n) (m>0)。
j当PO=PF时，分别求出点P和点Q的坐标；
k在j的基础上，当正方形ABCD左右平移时，请直接写出m的取值范围；
l当n=7时，是否存在m的值使点P为AB边中点。若存在，请求出m的值；若不存在，请说明理由。
某校男子足球队的年龄分布如下面的条形图所示．
（1）求这些队员的平均年龄；
（2）下周的一场校际足球友谊赛中，该校男子足球队将会有11名队员作为首发队员出场，不考虑其他因素，请你求出其中某位队员首发出场的概率．
我们把两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB=CB，AD=CD，请你写出与筝形ABCD的角或者对角线有关的一个结论，并证明你的结论．
先化简，再求值：
，其中a
5．
如图，在平面直角坐标系中，O为原点，平行四边形ABCD的边BC在x轴上，D点在y轴上，C点坐标为（2，0），BC=6，∠BCD=60°，点E是AB上一点，AE=3EB，⊙P过D，O，C三点，抛物线
过点D，B，C三点．
（1）求抛物线的解析式；
（2）求证：ED是⊙P的切线；
（3）若将△ADE绕点D逆时针旋转90°，E点的对应点E′会落在抛物线上吗？请说明理由；
（4）若点M为此抛物线的顶点，平面上是否存在点N，使得以点B，D，M，N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．
已知关于x的方程
．
（1）求证：无论k取任何实数时，方程总有实数根；
（2）当抛物线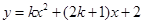
图象与x轴两个交点的横坐标均为整数，且k为正整数时，若P（a，
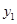），Q（1，
）是此抛物线上的两点，且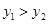
，请结合函数图象确定实数a的取值范围；
（3）已知抛物线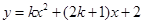恒过定点，求出定点坐标．