（本题共两小题，每小题5分，共10分）（1）已知集合A{x|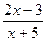-优题课

（本题共两小题，每小题5分，共10分）
（1）已知集合A={x|≤0}， B={x|x²－3x+2<0}， U=R，求（uA）∩ B．
（2）计算．

科目数学题型解答题难度较易

如图是一个直三棱柱（以 $A_{1} B_{1} C$ 为底面）被一平面所截得到的几何体，截面为 $A B C$ ．已知 $A_{1} B_{1} = B_{1} C_{1} = 1, ∠ A_{1} B_{1} C_{1} = 90^{o}, A A_{1} = 4, B B_{1} = 2, C C_{1} = 3$ ， $∠ A_{l} B_{l} C_{1} ＝ 90 °$ ，
$A A_{l} ＝ 4$ ， $B B_{l} ＝ 2$ ， $C C_{l} ＝ 3$ ．
（1）设点 $O$ 是 $A B$ 的中点，证明： $O C ∥$ 平面 $A_{1} B_{1} C_{1}$

（2）求二面角 $B - A C - A_{1}$ 的大小；
（3）求此几何体的体积．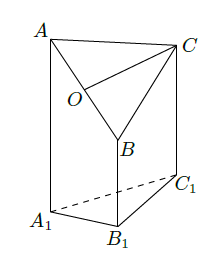

某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品，制作过程必须先后经过两次烧制，当第一次烧制合格后方可进入第二次烧制，两次烧制过程相互独立．根据该厂现有的技术水平，经过第一次烧制后，甲、乙、丙三件产品合格的概率依次为0.5，  0.6，  0.4．经过第二次烧制后，甲、乙、丙三件产品合格的概率依次为0.6，0.5，0.75．
（1）求第一次烧制后恰有一件产品合格的概率；
（2）经过前后两次烧制后，合格工艺品的个数为 $ξ$ ，求随机变量 $ξ$ 的期望．

如图,函数 $y = 2 \cos (ω x + θ) (x \in R, 0 \leq θ \leq \frac{π}{2})$ 的图象与 $y$ 轴交于点( $0, \sqrt{3}$ )，且在该点处切线的斜率为 $- 2$ ．
（1）求 $θ$ 和 $ω$ 的值；
（2）已知点 $A (\frac{π}{2}, 0)$ ，点 $P$ 是该函数图象上一点，点 $Q (x_{0}, y_{0})$ 是 $P A$ 的中点，当 $y_{0} = \frac{\sqrt{3}}{2}, x_{0} \in [\frac{π}{2}, π]$ 时，求 $x_{0}$ 的值．

已知函数 $f (x) = \{\begin{cases} c x + 1 (0 < x < c) \\ 2^{- \frac{x}{c^{2}}} + k (c \leq x < 1) \end{cases}$ 在区间(0，1)内连续,且 $f (c^{2}) = \frac{9}{8}$ ．
（1）求实数 $k$ 和 $c$ 的值；
（2）解不等式 $f (x) > \frac{\sqrt{2}}{8} + 1$

已知数列 $\{a_{n}\}$ 中 $a_{1} = 2, a_{n + 1} = (\sqrt{2} - 1) (a_{n} + 2), n = 1, 2, 3 . . . . . . . .$

（Ⅰ）求 $\{a_{n}\}$ 的通项公式；
（Ⅱ）若数列 $\{b_{n}\}$ 中 $b_{1_{}} = 2, b_{n + 1} = \frac{3 b_{n} + 4}{2 b_{n} + 3}, n = 1, 2, 3 . . . . . . .$ ，证明：
$\sqrt{2} < b_{n} \leq a_{4 n - 3}, n = 1, 2, 3 . . . . . . .$

试卷网试题网古诗词网作文网范文网