在如图8所示的方格图中,每个小正方形的顶点称为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:
图中格点 是由格点
是由格点 通过怎样变换得到的?
通过怎样变换得到的?
如果建立直角坐标系后,点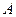 的坐标为(
的坐标为( ,
, ),点
),点 的坐标为
的坐标为 ,请求出过
,请求出过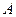 点的正比例函数的解析式,并写出图中格点
点的正比例函数的解析式,并写出图中格点 各顶点的坐标.
各顶点的坐标.
如图,直线AD与AB、CD相交于A、D两点,EC、BF与AB、CD相交于E、C、B、F,
如果∠1=∠2,∠B=∠C.
求证:∠A=∠D.
在图所示的平面直角坐标系中表示下面各点:
A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7)。
(1)A点到原点O的距离是__ __个单位长。(2)将点C向左平移6个单位,它会与点重合。
(3)连接CE,则直线CE与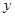 轴是什么位置关系?(4)点F到
轴是什么位置关系?(4)点F到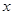 、
、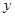 轴的距离分别是多少?
轴的距离分别是多少?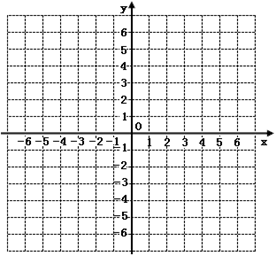
如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,A点在C处的北偏西45°方向,求∠BAC及∠BCA的度数. 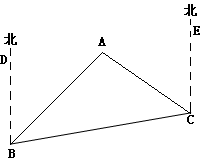
如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.
已知一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.