如图,直线AD与AB、CD相交于A、D两点,EC、BF与AB、CD相交于E、C、B、F,
如果∠1=∠2,∠B=∠C.
求证:∠A=∠D.
(11·曲靖)如图:直线y=kx+3与x轴、y轴分别交于A、B两点,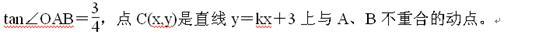 (1)求直线y=kx+3的解析式;
(1)求直线y=kx+3的解析式;
(2)当点C运动到什么位置时△AOC的面积是6;
(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?
若存在,请求出点C的坐标;若不存在,请说明理由。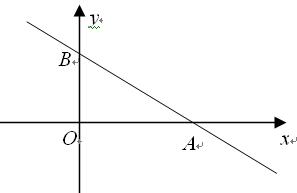
(11·曲靖)(10分)如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°。
(1)求∠B OC的度数;
OC的度数;
(2)求证:四边形AOBC是菱形。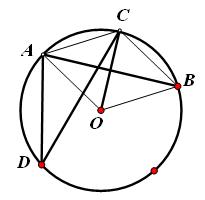
(11·曲靖)一名男生推铅球,铅球行进高度y(单位:m)与水平距离x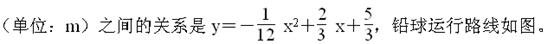
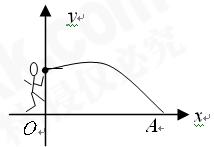
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m。
(11·曲靖)在三张完全相同的卡片上分别标注:A“一雨水”、B“大地”、
C“生机”,放入一个不透明的的口袋中,随机从中抽出一张放入“□给□带来□”左边“□”
内;第二次抽出一张放入中间的“□”内;第三次抽出一张放入右边的“□”内(每次卡片抽
出后不放回)。
(1)试用树形图列出三次抽卡出现的所有可能的结果表明;
(2)求其中恰好组成“雨水给大地带来生机”的概率。
( 11
11 ·曲靖)(9分)甲乙两个工程队合修一条公路,甲工程队比乙工程队每天多
·曲靖)(9分)甲乙两个工程队合修一条公路,甲工程队比乙工程队每天多
修50米,甲工程队修900米所用时间和乙工程队修600米所用时间相等,问甲乙两个工程
队每天分别修多少米?