((本小题满分12分)某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一 名学生被考官A面试的概率?
名学生被考官A面试的概率?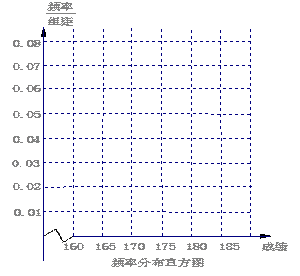
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
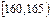 |
5 |
0.050 |
| 第2组 |
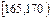 |
① |
0.350 |
| 第3组 |
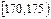 |
30] |
② |
| 第4组 |
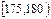 |
20 |
0.200 |
| 第5组 |
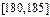 |
10 |
0.100 |
| 合计 |
1 00 00 |
1.00 |
若非零函数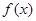 对任意实数
对任意实数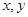 均有
均有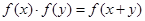 ,且当
,且当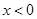 时
时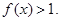
(1)求证: ;
;
(2)求证: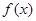 为R上的减函数;
为R上的减函数;
(3)当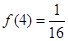 时, 对
时, 对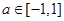 时恒有
时恒有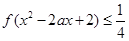 ,求实数
,求实数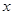 的取值范围.
的取值范围.
已知函数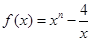 ,且
,且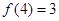 .
.
(1)判断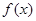 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)判断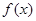 在区间
在区间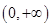 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若对任意实数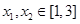 ,有
,有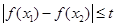 成立,求
成立,求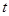 的最小值.
的最小值.
湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为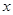 元,
元,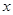 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润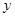 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格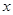 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每纪念章销售价格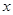 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润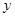 (元)最大,并求出最大值.
(元)最大,并求出最大值.
已知集合 与
与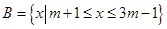 分别是函数
分别是函数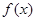 的定义域与值域.
的定义域与值域.
(1)求集合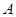 ;
;
(2)当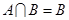 时,求实数
时,求实数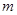 的取值范围.
的取值范围.
(1)计算: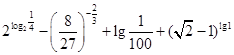
(2)已知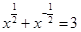 ,求
,求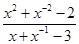 的值.
的值.