湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为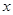 元,
元,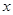 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润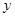 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格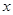 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每纪念章销售价格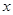 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润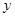 (元)最大,并求出最大值.
(元)最大,并求出最大值.
(本小题满分12分)
某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.
(I)求AB的长度;
(Ⅱ)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用最低,请说明理由.
(本小题满分10分)
已知等差数列{ },
}, 为其前n项的和,
为其前n项的和, =0,
=0, =6,n∈N*.
=6,n∈N*.
(I)求数列{ }的通项公式;
}的通项公式;
(II)若 =3
=3 ,求数列{
,求数列{ }的前n项的和.
}的前n项的和.
已知函数 .
.
(I)求函数 的单调区间;
的单调区间;
(Ⅱ)函数 在区间[1,2]上是否有零点,若有,求出零点,若没有,请说明理由;
在区间[1,2]上是否有零点,若有,求出零点,若没有,请说明理由;
(Ⅲ)若任意的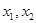 ∈(1,2)且
∈(1,2)且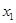 ≠
≠ ,证明:
,证明: (注:
(注: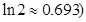
(本小题满分12分)已知焦点在 轴上的椭圆C1:
轴上的椭圆C1: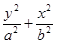 =1经过A(1,0)点,且离心率为
=1经过A(1,0)点,且离心率为 .
.
(I)求椭圆C1的方程;
(Ⅱ)过抛物线C2: (h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与
(h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与 轴平行时,求h的最小值.
轴平行时,求h的最小值.
(本小题满分12分)如图,在四棱锥P—ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AB,M、N分别是PA、BC的中点.
(I)求证:MN∥平面PCD;
(II)在棱PC上是否存在点E,使得AE上平面PBD?若存在,求出AE与平面PBC所成角的正弦值,若不存在,请说明理由