(本小题满分12分)已知焦点在 轴上的椭圆C1:
轴上的椭圆C1: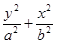 =1经过A(1,0)点,且离心率为
=1经过A(1,0)点,且离心率为 .
.
(I)求椭圆C1的方程;
(Ⅱ)过抛物线C2: (h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与
(h∈R)上P点的切线与椭圆C1交于两点M、N,记线段MN与PA的中点分别为G、H,当GH与 轴平行时,求h的最小值.
轴平行时,求h的最小值.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑.
(本小题满分10分)选修4-1:几何证明选讲
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
(I)证明:CD//AB;
(II)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
(本小题满分12分)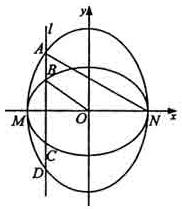
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A,B,C,D.
(I)设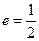 ,求
,求 与
与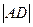 的比值;
的比值;
(II)当e变化时,是否存在直线l,使得BO∥AN,并说明理由.
(本小题满分12分)
设函数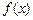 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=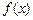 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;
(II)证明: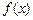 ≤2x-2.
≤2x-2.
(本小题满分12分)
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(I)假设n=2,求第一大块地都种植品种甲的概率;
(II)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据 的的样本方差
的的样本方差 ,其中
,其中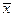 为样本平均数.
为样本平均数.
(本小题满分12分)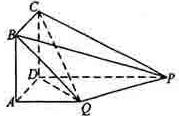
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB= PD.
PD.
(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q—ABCD的的体积与棱锥P—DCQ的体积的比值.