已知函数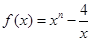 ,且
,且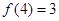 .
.
(1)判断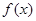 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)判断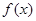 在区间
在区间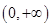 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若对任意实数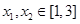 ,有
,有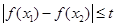 成立,求
成立,求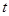 的最小值.
的最小值.
(本题满分16分)
数列{an}中, .
.
(1)求a1,a2,a3,a4;
(2)猜想an的表达式,并用数学归纳法加以证明.
假定某射手每次射击命中的概率为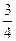 ,且只有
,且只有 发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
求:(1 )目标被击中的概率;
)目标被击中的概率;
(2) 的概率分布;
的概率分布;
(3)均值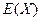 .
.
(本题满分15分,请列式并用数字表示结果,直接写结果不得分)
从5名女同学和4名男同学中选出4人参加四场不同的演讲,分别按下列要求,各有 多少种不同
多少种不同 选法?
选法?
(1)男、女同学各2名;
(2)男、女同学分别至少有1名;
(3)在(2)的前提下,男同学甲与女同学乙不能同时选出.
已知z为复数,z+2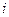 和
和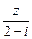 均为实数,其中
均为实数,其中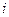 是虚数单位
是虚数单位 .
.
(1)求复数z;
(2)若复数 在复平面上对应的点在第一象限,求实数a的取值范围.
在复平面上对应的点在第一象限,求实数a的取值范围.
函数 的图象在
的图象在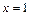 处的切线方程为
处的切线方程为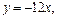
(1) 求函
求函 数
数 的解析式;
的解析式;
(2) 求函数 的单调递减区间。
的单调递减区间。