（本题满分8分，每小题4分）
袋子中装有2个红球，1个黄球，它们除颜色外其余都相同。小明和小英做摸球游戏，约定一次游戏规则是：小英先从袋中任意摸出1个球记下颜色后放回，小明再从袋中摸出1个球记下颜色后放回，如果两人摸到的球的颜色相同，小英赢，否则小明赢．
（1）请用树状图或列表格法表示一次游戏中所有可能出现的结果；
（2）这个游戏规则对双方公平吗？请说明理由.
（满分9分）如图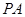
、
是半径为1的
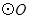的两条切线，点
、
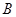分别为切点，
∠APB＝60°,OP与弦AB交于点C,与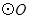交于点D.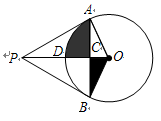
（1）在不添加任何辅助线的情况下，写出图中所有的全等三角形；
（2）求阴影部分的面积（结果保留
）．
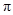用一个圆心角为80°,半径为4的扇形做一个圆锥，求这个圆锥的侧面积.（结果保留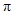
）
已知抛物线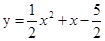
（1）求出它的顶点坐标和对称轴方程；
（2）若抛物线与x轴的两个交点为A、B，求线段AB的长。
(1)解方程：① x2+4x－12="0" ② 3x2+5(2x+1)=0
(2)计算：
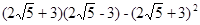
施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米.现以O点为原点，OM所在直线为X轴建立直角坐标系（如图所示）.
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数解析式；
（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下.