如图所示，静止在粗糙水平面上的斜面体有三个光滑斜面AB、AC和CD。已知斜面AB与水平方向成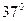
角，斜面AC与水平方向成
角，斜面CD与水平方向成
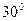角，A点与C点的竖直高度为
，C点与D点的竖直高度为
。在B点左侧的水平面上有一个一端固定的轻质弹簧，自然长度时弹簧右端到B点的水平距离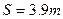为
。质量均为
的物体甲和乙同时从顶点A由静止释放，之后甲沿斜面AB下滑，乙沿AC下滑。在甲乙两物体下滑过程中，斜面体始终处于静止状态，且两物体运动中经过B点、C点、D点时，速度大小不改变，只改变方向。甲进入水平面后向左运动压缩弹簧的最大压缩量为
，乙物体进入水平面后便向右运动最终停止。已知甲物体与水平面的动摩擦因数为
，（
）求：
（1）弹簧的最大弹性势能为多少？
（2）甲物体最终停止位置距B点多远？
（3）通过计算，说明甲乙两物体是否同时滑到水平面上？
（4）若以释放甲乙物体时作为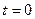
时刻，做出斜面体受到地面的摩擦力大小
随时间变化的图线。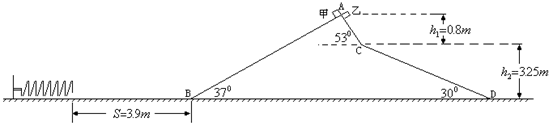
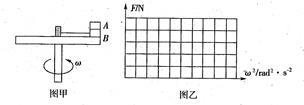
如图甲所示，水平转盘可绕竖直中心轴转动，盘上叠放着质量均为1kg的A、B两个物块，B物体用长为0.25m的细线与固定在转盘中心处的力传感器相连，两个物块和传感器的大小均可忽略不计，细线能承受的最大拉力为8N，A、B间的动摩擦因数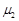
=0.4，B与转盘间的动摩擦因素
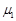=0.1，且可认为最大静摩擦力等于滑动摩擦力。转盘静止时，细线刚好伸直，力传感器的读数为零，当转盘以不同的角速度匀速转动时，力传感器上就会显示相应的读数F。试通过计算在图乙的坐标系中作出
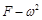的图象，g取
如下图所示，离地面足够高处有一竖直的空心管，质量为2kg，管长为24m，M、N为空心管的上、下两端，空心管受到大小为16N的竖直向上的拉力作用，由静止开始竖直向下做匀加速运动，同时在M处有一个大小不计的小球沿管的轴线做竖直上抛运动，取g＝10m/s2。若小球上抛的初速度为10m/s，试问：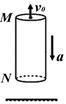
（1）经过多少秒小球从管的N端穿出。
（2）若此空心管的N端距离地面高为64m，欲使在空心管到达地面时小球刚好进入管内，在其他条件不变的前提下，则小球初速度大小应为多大？
如下图所示，斜面AB与竖直半圆轨道在B点圆滑相连，斜面倾角为θ=45°，半圆轨道的半径为R，一小球从斜面的顶点A由静止开始下滑，进入半圆轨道，最后落到斜面上，不计一切摩擦。试求：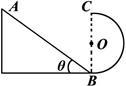
（1）欲使小球能通过半圆轨道最高点C，落到斜面上，斜面AB的长度L至少为多大？
（2）在上述最小L的条件下，小球从A点由静止开始运动，最后落到斜面上的落点与半圆轨道直径BC的距离x为多大？
如图所示，底座A上装有L="0.5" m长的直立杆，底座和杆的总质量为M="2.0" kg，底座高度不计，杆上套有质量为m="0.2" kg的小环B，小环与杆之间有大小恒定的摩擦力．当小环从底座上以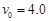
m/s的初速度向上飞起时，恰好能到达杆顶，然后沿杆下降，取g="10" m/s2，求：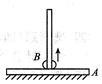
(1)在环飞起过程中，底座对水平面的压力；
(2)此环下降过程需要多长时间．
如图所示，光滑杆AB长为L，B端固定一根劲度系数为k、原长为l0的轻弹簧，质量为m的小球套在光滑杆上并与弹簧的上端连接．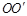
为过B点的竖直轴，杆与水平面间的夹角始终为θ．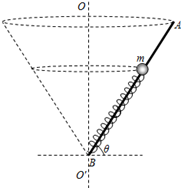
（1）杆保持静止状态，让小球从弹簧的原长位置静止释放，求小球释放瞬间的加速度大小a及小球速度最大时弹簧的压缩量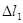
；
（2）当球随杆一起绕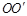轴匀速转动时，弹簧伸长量为
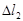，求匀速转动时的角速度ω；
（3）若θ=30°，移去弹簧，当杆绕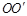轴以角速度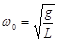
匀速转动时，小球恰好在杆上某一位置随杆在水平面内匀速转动，球受到轻微扰动后沿杆向上滑动，到最高点A时球沿杆方向的速度大小为v0，求小球从开始滑动到离开杆的过程中，杆对球所做的功W．