(本小题12分)如图,四棱锥P-ABCD是底面边长为1的正方形,PD ⊥BC,PD=1,PC= .
.
(Ⅰ)求证:PD⊥面ABCD;
(Ⅱ)求二面角A-PB-D的大小.
已知过点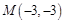 的直线
的直线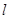 与圆
与圆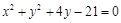 相交于
相交于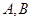 两点,若弦
两点,若弦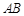 的长为
的长为 ,求直线
,求直线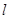 的方程;
的方程;
如图,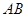 是底部
是底部 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物,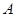 为塔的最高点.现需在对岸测出塔高
为塔的最高点.现需在对岸测出塔高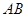 ,甲、乙两同学各提出了一种测量方法.
,甲、乙两同学各提出了一种测量方法.
甲同学的方法是:选与塔底 在同一水平面内的一条基线
在同一水平面内的一条基线 ,使
,使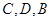 三点不在同一
三点不在同一
条直线上,测出 及
及 的大小(分别用
的大小(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用 表示测得的数据),另外需在点
表示测得的数据),另外需在点 测得塔顶
测得塔顶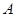 的仰角(用
的仰角(用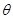 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高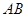 .
.
乙同学的方法是:选一条水平基线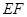 ,使
,使 三点在同一条直线上.在
三点在同一条直线上.在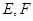 处分别测得塔顶
处分别测得塔顶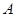 的仰角(分别用
的仰角(分别用 表示测得的数据)以及
表示测得的数据)以及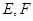 间的距离(用
间的距离(用 表示测得的数据),就可以求得塔高
表示测得的数据),就可以求得塔高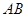 .
.
请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时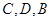 按逆时针方向标注,
按逆时针方向标注,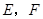 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高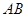 .
.
一光线从点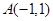 发出射向
发出射向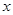 轴,被
轴,被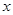 轴反射后,使点
轴反射后,使点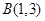 到反射线的距离为
到反射线的距离为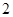 ,求反射线所在直线方程.
,求反射线所在直线方程.
在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中,
( I )求成绩在区间[80,90)内的学生人数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100] 内的概率。
已知 ,且
,且 是第二象限角,求
是第二象限角,求 的值。
的值。