(本小题满分12分) 直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的方程为
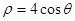 ,直线
,直线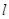 方程为
方程为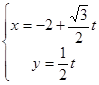 (t为参数),直线
(t为参数),直线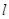 与C的公共点为T.
与C的公共点为T.
(1)求点T的极坐标;
(2)过点T作直线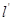 ,
,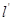 被曲线C截得的线段长为2,求直线
被曲线C截得的线段长为2,求直线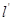 的极坐标方程.
的极坐标方程.
(本小题满分12分)
已知圆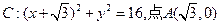 ,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。
,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。
(I)求轨迹E的方程;
(II)过点P(1,0)的直线 交轨迹E于两个不同的点A、B,
交轨迹E于两个不同的点A、B, (O是坐标原点)的面积
(O是坐标原点)的面积 ,求直线AB的方程。
,求直线AB的方程。
(本小题满分12分)
已知函数
(I)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(II)求证: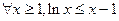 ;
;
(III)已知数列 若
若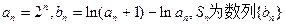 的前n项和,求证:
的前n项和,求证:
(本小题满分12分)
如图,正方形ADEF所在平面和等腰梯形所在平面AB CD垂直,已知BC=2AD=4,
CD垂直,已知BC=2AD=4, ,
,
(I)求证: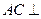 面ABF;
面ABF;
(II)求异面直线BE与AF所成的角;
(III)求该几何体的表面积。
(本小题满分12分)
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,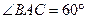 ,在A地听到弹射声音的时间比B地晚
,在A地听到弹射声音的时间比B地晚 秒,A地测得该仪器在A、B、C三地位于同一水平面上,至最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)
秒,A地测得该仪器在A、B、C三地位于同一水平面上,至最高点H时的仰角为30°,求该仪器的垂直弹射高度CH(声音的传播速度为340米/秒)
(本小题满分10分)
已知函数 .
.
(1)求函数 的定义域;(2)判断
的定义域;(2)判断 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使 ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间 的长度
的长度 ).
).