已知定点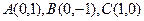 ,动点
,动点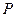 满足
满足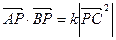 ,
,
(1)求动点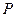 的轨迹方程,并说明方程表示什么曲线;
的轨迹方程,并说明方程表示什么曲线;
(2)当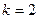 时,求
时,求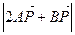 的最大值和最小值。
的最大值和最小值。
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N (点M在点N的右侧),且 。椭圆D:
。椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

( I ) 求圆C和椭圆D的方程;
(Ⅱ) 若过点M的动直线 与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线
与椭圆D交于A、B两点,若点N在以弦AB为直径的圆的外部,求直线 斜率的范围。
斜率的范围。
高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是 ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是 .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求 的分布列和数学期望.
的分布列和数学期望.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且 .
.
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)求二面角E-BC1-D的余弦值.
各项均为正数的等比数列{an}中,已知a2="8," a4="128," bn=log2an.
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Sn
(3)求满足不等式 的正整数n的最大值
的正整数n的最大值
已知 ,
, ,直线
,直线 与函数
与函数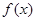 、
、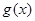 的图象都相切,且与函数
的图象都相切,且与函数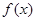 的图象的切点的横坐标为
的图象的切点的横坐标为 .
.
(Ⅰ)求直线 的方程及
的方程及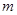 的值;
的值;
(Ⅱ)若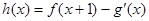 (其中
(其中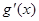 是
是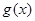 的导函数),求函数
的导函数),求函数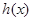 的最大值;
的最大值;
(Ⅲ)当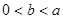 时,求证:
时,求证: .
.