(本小题满分12分)
某市4997名学生参加高中数学会考,得分均在60分以上,现从中随机抽取一个容量为500的样本,制成如图a所示的频率分布直方图

(1)由频率分布直方图可知本次会考的数学平均分为81分.请估计该市得分在区间[60,70]的人数;
(2)如图b所示茎叶图是某班男女各4名学生的得分情况,现用简单随机抽样的方法,从这8名 学生中,抽取男女生各一人,求女生得分不低于男生得分的概率.
学生中,抽取男女生各一人,求女生得分不低于男生得分的概率.
选修4—4:坐标系与参数方程.
坐标系与参数方程在直角坐标系xOy中,圆C的参数方程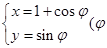 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)射线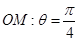 与圆C的交点为O、P两点,求P点的极坐标.
与圆C的交点为O、P两点,求P点的极坐标.
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连结AE,BE.证明: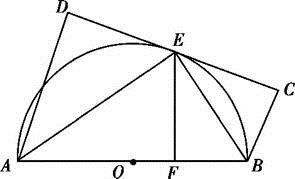
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
(本小题满分12分)
设函数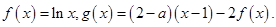
(Ⅰ)当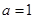 时,求函数
时,求函数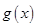 的单调区间;
的单调区间;
(Ⅱ)若对任意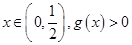 恒成立,求实数
恒成立,求实数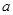 的最小值;
的最小值;
(Ⅲ)设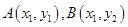 是函数
是函数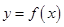 图象上任意不同两点,线段AB中点为C
图象上任意不同两点,线段AB中点为C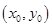 ,直线AB的斜率为k.证明:
,直线AB的斜率为k.证明: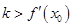 .
.
(本小题满分12分)已知离心率为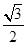 的椭圆
的椭圆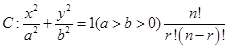 与直线
与直线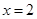 相交于
相交于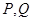 两点(点
两点(点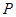 在
在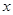 轴上方),且
轴上方),且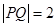 .点
.点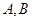 是椭圆上位于直线
是椭圆上位于直线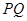 两侧的两个动点,且
两侧的两个动点,且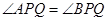 .
.
(Ⅰ)求椭圆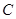 的标准方程;
的标准方程;
(Ⅱ)求四边形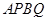 面积的取值范围.
面积的取值范围.
(本小题满分12分)小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.