(本小题满分12分)小王在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次发放1个.
(Ⅰ)若小王发放5元的红包2个,求甲恰得1个的概率;
(Ⅱ)若小王发放3个红包,其中5元的2个,10元的1个.记乙所得红包的总钱数为X,求X的分布列和期望.
已知向量a= ,b=
,b= ,且x∈
,且x∈ .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值为- ,求正实数λ的值.
,求正实数λ的值.
若复数z1与z2在复平面上所对应的点关于y轴对称,且z1(3-i)=z2(1+3i),|z1|=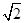 ,求z1.
,求z1.
A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
(1)求 ·
·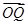 +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin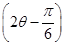 的值.
的值.
已知△ABC的内角A,B,C所对的边分别是a,b,c,设向量m=(a,b),n=(sin B,sin A),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p,边长c=2,C=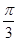 ,求△ABC的面积.
,求△ABC的面积.
已知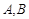 分别是椭圆
分别是椭圆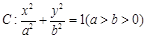 的左,右顶点,点
的左,右顶点,点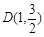 在椭圆
在椭圆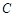 上,且直线
上,且直线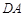 与直线
与直线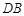 的斜率之积为
的斜率之积为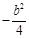 .
.
(1)求椭圆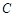 的标准方程;
的标准方程;
(2)点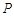 为椭圆
为椭圆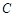 上除长轴端点外的任一点,直线
上除长轴端点外的任一点,直线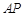 ,
, 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点 ,
,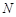 .
.
①在 轴上是否存在一个定点
轴上是否存在一个定点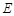 ,使得
,使得 ?若存在,求点
?若存在,求点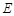 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②已知常数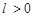 ,求
,求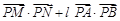 的取值范围.
的取值范围.