(本小题满分14分)
已知数列 是首项为
是首项为 ,公差为
,公差为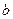 的等差数列,
的等差数列, 是首项为
是首项为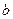 ,公比为
,公比为 的等比数列,且满足
的等比数列,且满足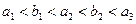 ,其中
,其中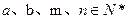 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若数列 与数列
与数列 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列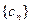 ,求数列
,求数列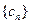 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列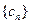 的前项之和为
的前项之和为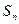 ,求证:
,求证: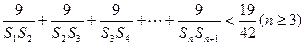
设 ,其导函数
,其导函数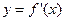 的图像经过点
的图像经过点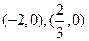 ,且在
,且在 时取得极小值
时取得极小值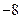 ,
,
(1)求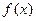 的解析式;
的解析式;
(2)若对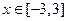 都有
都有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
如图,正三棱柱 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为 ,点
,点 在棱
在棱 上.
上.
(1)若 ,求证:直线
,求证:直线 平面
平面 ;
;
(2)若 ,二面角
,二面角 平面角的大小为
平面角的大小为 ,求
,求 的值。
的值。
 、
、 、
、 为
为 的三内角,且其对边分别为a、b、c,若
的三内角,且其对边分别为a、b、c,若 ,
, ,且
,且 .
.
(1)求角 ;
;
(2)若 ,三角形面积
,三角形面积 ,求
,求 的值.
的值.
对 ,不等式
,不等式 所表示的平面区域为
所表示的平面区域为 ,把
,把 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
(1)求 ,
, ;
;
(2)数列 满足
满足 ,且
,且 时
时 .证明当
.证明当 时,
时, ;
;
(3)在(2)的条件下,试比较 与4的大小关系.
与4的大小关系.
已知 过定点
过定点 ,圆心
,圆心 在抛物线
在抛物线 :
: 上运动,
上运动, 为圆
为圆 在
在 轴上所截得的弦.
轴上所截得的弦.
⑴当 点运动时,
点运动时, 是否有变化?并证明你的结论;
是否有变化?并证明你的结论;
⑵当 是
是 与
与 的等差中项时,
的等差中项时,
试判断抛物线 的准线与圆
的准线与圆 的位置关系,
的位置关系,
并说明理由。