如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径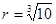 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
(1)如果瓶内的药液恰好 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为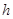 (单位:厘米),已知当
(单位:厘米),已知当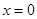 时,
时,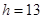 .试将
.试将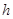 表示为
表示为 的函数.(注:
的函数.(注: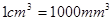 )
)
已知函数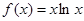 ,
,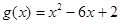 。
。
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数 在区间
在区间
 上的最小值;
上的最小值;
(Ⅲ)试判断方程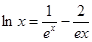 (其中
(其中 )是否有实数解?并说明理由。
)是否有实数解?并说明理由。
甲箱中放有 个红球与
个红球与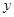 个白球(
个白球(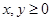 ,且
,且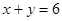 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
(Ⅰ)记取出的3个球颜色全不相同的概率为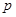 ,求当
,求当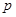 取得最大值时的
取得最大值时的 ,
,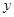 的值;
的值;
(Ⅱ)当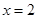 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数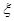 的期望
的期望 。
。
用0,1,2,3,4这五个数字组成无重复数字的自然数。
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数。
已知数列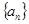 满足
满足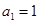 ,且
,且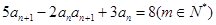 。
。
(Ⅰ)求 ,
,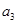 ,
, 的值;
的值;
(Ⅱ)猜想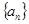 的通项公式,并用数学归纳法证明你的猜想。
的通项公式,并用数学归纳法证明你的猜想。
已知复数 (
( 为虚数单位)
为虚数单位)
(Ⅰ)把复数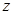 的共轭复数记作
的共轭复数记作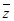 ,若
,若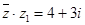 ,求复数
,求复数 ;
;
(Ⅱ)已知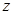 是关于
是关于 的方程
的方程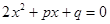 的一个根,求实数
的一个根,求实数 ,
, 的值。
的值。