(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分.)
已知数列{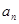 }满足:
}满足: ,
, 为数列
为数列 的前
的前 项和。
项和。
(1) 若{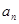 }是递增数列,且
}是递增数列,且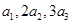 成等差数列,求
成等差数列,求 的值;
的值;
(2) 若 ,且{
,且{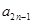 }是递增数列,{
}是递增数列,{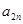 }是递减数列,求数列{
}是递减数列,求数列{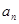 }的通项公式;
}的通项公式;
(3) 若 ,对于给定的正整数
,对于给定的正整数 ,是否存在一个满足条件的数列
,是否存在一个满足条件的数列 ,使得
,使得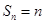 ,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
,如果存在,给出一个满足条件的数列,如果不存在,请说明理由。
已知命题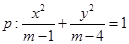 表示双曲线,命题
表示双曲线,命题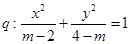 表示椭圆.
表示椭圆.
⑴若命题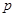 为真命题,求实数
为真命题,求实数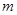 的取值范围.
的取值范围.
⑵判断命题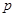 为真命题是命题
为真命题是命题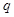 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
根据我国发布的《环境空气质量指数 技术规定》(试行),
技术规定》(试行), 共分为六级:
共分为六级: 为优,
为优,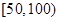 为良,
为良,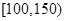 为轻度污染,
为轻度污染,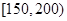 为中度污染,
为中度污染, 均为重度污染,
均为重度污染,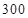 及以上为严重污染.某市2013年11月份
及以上为严重污染.某市2013年11月份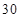 天的
天的 的频率分布直方图如图所示:
的频率分布直方图如图所示: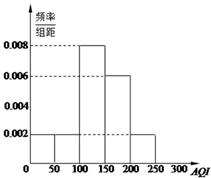
⑴该市11月份环境空气质量优或良的共有多少天?
⑵若采用分层抽样方法从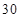 天中抽取
天中抽取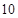 天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
天进行市民户外晨练人数调查,则中度污染被抽到的天数共有多少天?
⑶空气质量指数低于 时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
时市民适宜户外晨练,若市民王先生决定某天早晨进行户外晨练,则他当天适宜户外晨练的概率是多少?
在平面直角坐标系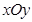 中,已知点
中,已知点 ,
, 是动点,且
是动点,且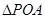 的三边所在直线的斜率满足
的三边所在直线的斜率满足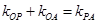 .
.
(1)求点 的轨迹
的轨迹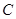 的方程;
的方程;
(2)若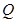 是轨迹
是轨迹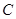 上异于点
上异于点 的一个点,且
的一个点,且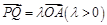 ,直线
,直线 与
与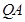 交于点
交于点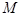 ,问:是否存在点
,问:是否存在点 ,使得
,使得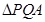 和
和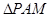 的面积满足
的面积满足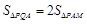 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,平面 平面
平面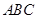 ,
,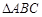 是等腰直角三角形,
是等腰直角三角形, ,四边形
,四边形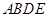 是直角梯形,
是直角梯形,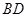 ∥AE,
∥AE,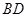

 ,
, ,
,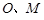 分别为
分别为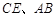 的中点.
的中点.
(1)求异面直线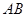 与
与 所成角的大小;
所成角的大小;
(2)求直线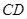 和平面
和平面 所成角的正弦值.
所成角的正弦值.
已知圆 的极坐标方程是
的极坐标方程是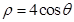 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线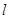 的参数方程是
的参数方程是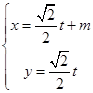 (
( 是参数).若直线
是参数).若直线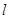 与圆
与圆 相切,求实数
相切,求实数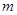 的值.
的值.