已知函数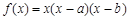 ,点
,点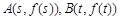 .
.
(1)若 ,函数
,函数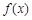 在
在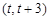 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求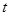 的取值范围;
的取值范围;
(2)当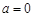 时,
时, 对任意的
对任意的 恒成立,求
恒成立,求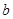 的取值范围;
的取值范围;
(3)若 ,函数
,函数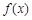 在
在 和
和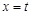 处取得极值,且
处取得极值,且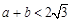 ,
,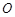 是坐标原点,证明:直线
是坐标原点,证明:直线 与直线
与直线 不可能垂直.
不可能垂直.
如图所示,四棱锥P-ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,
又棱PA=AB=2,E为CD的中点,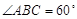 .
.
(Ⅰ)求证:直线EA⊥平面PAB;
(Ⅱ)求直线AE与平面PCD所成角的正切值.
已知圆C的圆心在坐标原点,且被直线3x+4y+15=0截得的弦长为8
(Ⅰ)试求圆C的方程;
(Ⅱ)当P在圆C上运动时,点D是P在x轴上的投影,M为线段PD上一点,且|MD|= |PD|.求点M的轨迹方程;
|PD|.求点M的轨迹方程;
命题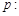 实数x满足
实数x满足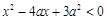 (其中
(其中 ),命题
),命题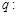
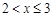
(Ⅰ)若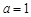 ,且
,且 为真,求实数
为真,求实数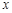 的取值范围;
的取值范围;
(Ⅱ)若q是p的充分不必要条件,求实数a的取值范围.
(本小题14分)
已知函数f(x)=ax3+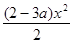 +bx(a,b为常数)
+bx(a,b为常数)
1) 若y=f(x)的图象在x=2处的切线方程为x-y+6=0,求函数y=f(x)的解析式;
2) 在1)的条件下,讨论函数y=f(x)的图象与函数y =- [f /(x)-9x-3]+m的图象的交点的个数;
[f /(x)-9x-3]+m的图象的交点的个数;
3) 当a=1时, ,lnx ≤f /(x)恒成立,求实数b的取值范围。
,lnx ≤f /(x)恒成立,求实数b的取值范围。
(本小题12分)
已知椭圆C的中心在原点,焦点在x轴上,离心率等于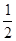 ,它的一个顶点恰好是抛物线x2 =
,它的一个顶点恰好是抛物线x2 =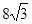 y的焦点。
y的焦点。
1)求椭圆C的方程;
2)点P(2,3),Q(2,-3)在椭圆上,A、B是椭圆上位于直线PQ两侧的动点。
(1)若直线AB的斜率为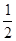 ,求四边形APBQ的面积的最大值;
,求四边形APBQ的面积的最大值;
(2)当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由;