(本小题共14分)如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.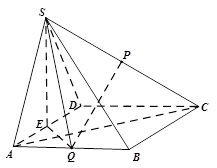
(Ⅰ)求证:PQ∥平面SAD;
(Ⅱ)求证:AC⊥平面SEQ;
(Ⅲ)如果SA=AB=2,求三棱锥S-ABC的体积.
(本小题满分14分)某商店如果将进价为8元的商品按每件10元售出,每天可销售200件,现在提高售价以赚取更多利润.已知每涨价0.5元,该商店的销售量会减少10件,问将售价定为多少时,才能使每天的利润最大?其最大利润为多少?
已知函数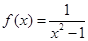 .
.
(1)设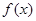 的定义域为A,求集合A;
的定义域为A,求集合A;
(2)判断函数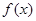 在(1,+
在(1,+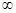 )上单调性,并用定义加以证明.
)上单调性,并用定义加以证明.
计算:
(1)集合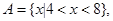 集合
集合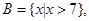 求
求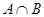 和
和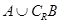
(2)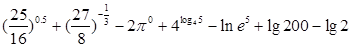
已知数列 的前
的前 项和为
项和为 ,且
,且 。
。
(1)求数列 的通项公式与前
的通项公式与前 项的和
项的和 ;
;
(2)设 ,若集合
,若集合 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围。
的取值范围。
某校高中三个年级共有学生1800名,各年级男生、女生的人数如下表:
| 高一年级 |
高二年级 |
高三年级 |
|
| 男生 |
290 |
b |
344 |
| 女生 |
260 |
c |
 |
已知在高中学生中随机抽取一名同学时,抽到高三年级女生的概率为0.17.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全校抽取60名学生,则在高二年级应抽取多少名学生?
(3)已知 ,求高二年级男生比女生多的概率。
,求高二年级男生比女生多的概率。