某校高中三个年级共有学生1800名,各年级男生、女生的人数如下表:
| |
高一年级 |
高二年级 |
高三年级 |
| 男生 |
290 |
b |
344 |
| 女生 |
260 |
c |
 |
已知在高中学生中随机抽取一名同学时,抽到高三年级女生的概率为0.17.
(1)求 的值;
的值;
(2)现用分层抽样的方法在全校抽取60名学生,则在高二年级应抽取多少名学生?
(3)已知 ,求高二年级男生比女生多的概率。
,求高二年级男生比女生多的概率。
设椭圆C1: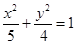 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点)。如图,若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点)。如图,若抛物线C2: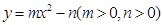 与y轴的交点为B,且经过F1,F2两点。
与y轴的交点为B,且经过F1,F2两点。
1.求抛物线C2的方程;
2.设M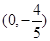 ,N为抛物线C2上的动点,过点N作抛物线C2的切线交椭圆C1于点P、Q两点,求△MPQ面积的最大值。
,N为抛物线C2上的动点,过点N作抛物线C2的切线交椭圆C1于点P、Q两点,求△MPQ面积的最大值。
在直三棱柱ABC—A1B1C1中,AB=AC=AA1=6,BC=4,D是BC的中点,F是C1C上一点,且CF=4。
(1)求证:B1F⊥平面ADF;
(2)求三棱锥D—AB1F的体积;
(3)试在AA1上找一点E,使得BE//平面ADF。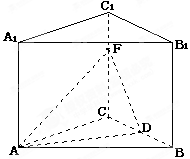
已知双曲线C: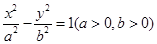 的离心率为
的离心率为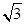 ,左顶点为(-1,0)。
,左顶点为(-1,0)。
(1)求双曲线方程;
(2)已知直线x-y+m=0与双曲线C交于不同的两点A、B,且线段AB的中点在圆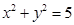 上,求m的值和线段AB的长。
上,求m的值和线段AB的长。
命题p:实数x满足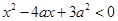 ,其中a<0;命题q:实数x满足
,其中a<0;命题q:实数x满足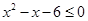 或
或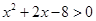 ,且
,且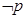 是
是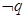 的必要不充分条件,求a的取值范围。
的必要不充分条件,求a的取值范围。
以下茎叶图记录了甲、乙两组四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中以X表示。
(1)如果X=8,求乙组同学植树棵数的平均数和标准差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率。