某超市为促销商品,特举办“购物有奖100﹪中奖”活动,凡消费者在该超市购物满100元,享受一次摇奖机会,购物满200元,享受两次摇 奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落。小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为20元,落入B袋为二等奖,奖金为10元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落。小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为20元,落入B袋为二等奖,奖金为10元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
(Ⅰ)求:摇奖两次,均获得一等奖的概率;
(Ⅱ)某消费者购物满200元,摇奖后所得奖金为X元,试求X的分布列与期望;
(Ⅲ)若超市同时举行购物八八折让利于消费者活动(打折后不再享受摇奖),某消费者刚好消费200元,请问他是选择摇奖还是选择打折比较划算.
已知函数
(1)若 ,求
,求 的值;
的值;
(2)求 的值.
的值.
已知椭圆
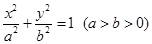 的左、右焦点分别为
的左、右焦点分别为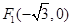 、
、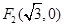 ,椭圆上的点
,椭圆上的点 满足
满足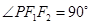 ,且
,且 的面积
的面积 .
.
(Ⅰ)求椭圆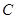 的方程;
的方程;
(Ⅱ)是否存在直线 ,使
,使 与椭圆
与椭圆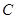 交于不同的两点
交于不同的两点 、
、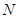 ,且线段
,且线段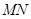 恰被直线
恰被直线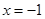 平分?若存在,求出
平分?若存在,求出 的斜率取值范围;若不存在,请说明理由.
的斜率取值范围;若不存在,请说明理由.
经调查统计,某种型号的汽车在匀速行驶中,每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度 (千米/时)的函数可表示为
(千米/时)的函数可表示为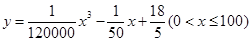 .已知甲、乙两地相距
.已知甲、乙两地相距 千米,在匀速行驶速度不超过
千米,在匀速行驶速度不超过 千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为
千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为 (升).
(升).
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)讨论函数 的单调性,当
的单调性,当 为多少时,耗油量
为多少时,耗油量 为最少?最少为多少升?
为最少?最少为多少升?
如图,四棱锥 中,底面
中,底面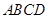 是菱形,
是菱形,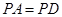 ,
,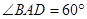 ,
,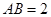 ,
,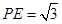 ,
,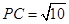 ,
, 是
是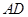 的中点,
的中点,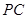 上的点
上的点 满足
满足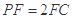 .
.
(Ⅰ)求证: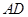
 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
在 中,角
中,角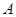 、
、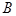 、
、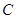 的对边分别为
的对边分别为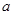 、
、 、
、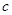 ,且
,且 .
.
(Ⅰ)求角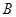 的大小;
的大小;
(Ⅱ)求 的取值范围.
的取值范围.