已知△ABC中,角A,B,C所对的边分别是a,b,c,且2(a2+b2﹣c2)=3ab;
(1)求 ;
;
(2)若c=2,求△ABC面积的最大值.
已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
设函数f(x)=ax2+(b﹣2)x+3(a≠0)
(1)若不等式f(x)>0的解集(﹣1,3).求a,b的值;
(2)若f(1)=2,a>0,b>0求 +
+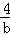 的最小值.
的最小值.
已知命题p:“存在 ”,命题q:“曲线
”,命题q:“曲线 表示焦点在x轴上的椭圆”,命题s:“曲线
表示焦点在x轴上的椭圆”,命题s:“曲线 表示双曲线”
表示双曲线”
(1)若“p且q”是真命题,求m的取值范围;
(2)若q是s的必要不充分条件,求t的取值范围.
已知函数f(x)=x2+xlnx.
(1)求f′(x);
(2)求函数f(x)图象上的点P(1,1)处的切线方程.