某商店储存的50个灯泡中,甲厂生产的灯泡占60%,乙厂生产的灯泡占40%,甲厂生产的灯泡的一等品率是90%,乙厂生产的灯泡的一等品率是80%.
(1)若从这50个灯泡中随机抽取出1个灯泡(每个灯泡被取出的机会均等),则它是甲厂生产的一等品的概率是多少?
(2)若从这50个灯泡中随机抽取出2个灯泡(每个灯泡被取出的机会均等),这2个灯泡中是甲厂生产的一等品的个数记为ξ,求E(ξ)的值.
近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨.现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为50%,后2天均为80%,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
(1)求至少有1天需要人工降雨的概率.
(2)求不需要人工降雨的天数x的分布列和期望.
一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于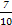 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
(1)求该射手恰好命中一次的概率.
(2)求该射手的总得分X的分布列.
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin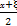 π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.