请同学们认真阅读下面材料,然后解答问题。
解方程(x2-1)2-5(x-1)+4=0
解:设y=x2-1
则原方程化为:y2-5y+4=0 ① ∴y1=1 y2=4
当y=1时,有x2-1=1,即x2=2 ∴x=±
当y=4时,有x2-1=4,即x2=5 ∴x=±
∴原方程的解为:x1=- x2=
x2= x3=-
x3=- x4=
x4=
解答问题:
⑴填空:在由原方程得到①的过程中,利用________________法达到了降次的目的,体现了________________的数学思想。
⑵解方程 -3(
-3( -3)=0
-3)=0
如图,在△ABC中,∠A=50°,DE//BC,∠BDE-∠B=20°,求∠AED的度数.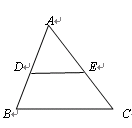
如图,已知直线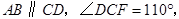 且
且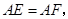 求
求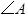 的度数.
的度数.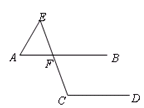
画图题
①已知线段m和n,请用直尺和圆规作出等腰△ABC,使得AB=AC, BC=m,∠A的平分线等于n.(只保留作图痕迹,不写做法)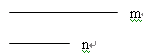
②如图,在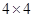 方格中画出所有以AB为一边的等腰Rt△ABC。(要求点C也在格点上)
方格中画出所有以AB为一边的等腰Rt△ABC。(要求点C也在格点上)
如图,∠CDG = ∠B,AD平分∠BAC,请说明△AGD是等腰三角形。请将过程填写完整。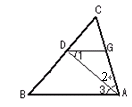
解:∵ ∠CDG = ∠B
∴ DG∥AB()
∴ ∠1 = ()
∵ AD平分∠BAC
∴ ()
∴∠1 = ∠2
∴△AGD是等腰三角形()
如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?