(本小题满分12分)
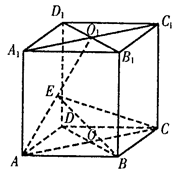
如图,直平行六面体ABCD-A1B1C1D1的高为3,
底面是边长为4, 且∠BAD=60°的菱形,AC∩
BD=O,A1C1∩B1D1=O1,E是线段AO1上一点.
(Ⅰ)求点A到平面O1BC的距离;
(Ⅱ)当AE为何值时,二面角E-BC-D的大小为 .
.
某班主任对全班50名学生进行了作业量多少的调查.数据如下表:
| 认为作业多 |
认为作业不多 |
合计 |
|
| 喜欢玩游戏 |
18 |
9 |
|
| 不喜欢玩游戏 |
8 |
15 |
|
| 合计 |
(1)请完善上表中所缺的有关数据;
(2)试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系?
附:
| P(K2≥K0) |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| K0 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |

已知数列 是公差不为0的等差数列,
是公差不为0的等差数列,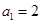 ,且
,且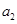 ,
, ,
,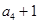 成等比数列.
成等比数列.
(1)求数列{an}的通项公式;
(2)设 ,求数列
,求数列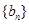 的前
的前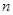 项和
项和 。
。
设向量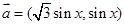 ,
,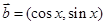 ,
,
(1)若 ,求
,求 的值;
的值;
(2)设函数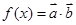 ,求
,求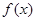 的最大值。
的最大值。
已知函数 与函数
与函数 在点
在点 处有公共的切线,设
处有公共的切线,设
 .
.
(1) 求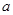 的值
的值
(2)求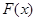 在区间
在区间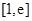 上的最小值.
上的最小值.
已知椭圆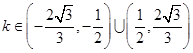 的焦点在
的焦点在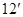 轴上,离心率为
轴上,离心率为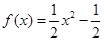 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点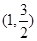 .
.
(1)求椭圆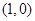 的方程;
的方程;
(2)直线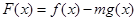 与椭圆
与椭圆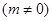 相交于
相交于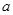 、
、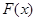 两点,
两点, 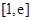 为原点,在
为原点,在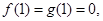 、
、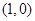 上分别存在异于
上分别存在异于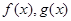 点的点
点的点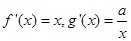 、
、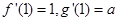 ,使得
,使得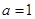 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率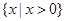 的取值范围.
的取值范围.