(本小题满分10分)
某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数: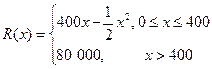 ,其中
,其中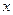 是仪器的月产量.
是仪器的月产量.
(1)将利润 元表示为月产量
元表示为月产量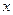 台的函数;
台的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润是多少?(总收益=总成本+利润)
(本小题满分14分)如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.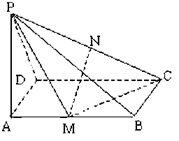
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
(本小题满分14分)
(1)已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中点为D,求AC边上中线BD所在的直线方程并化为一般式;
(2)已知圆C的圆心是直线 和
和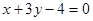 的交点且与直线
的交点且与直线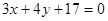 相切,求圆C的方程.
相切,求圆C的方程.
(本小题满分14分) 已知函数
(1)求函数 的最小正周期;
的最小正周期;
(2)确定函数 在
在 上的单调性并求在此区间上
上的单调性并求在此区间上 的最小值.
的最小值.
(本小题满分12分)某公司将进货单价为8元一个的商品按10元一个出售,每天可以卖出100个,若这种商品的售价每个上涨1元,则销售量就减少10个.
(1)求售价为13元时每天的销售利润;
(2)求售价定为多少元时,每天的销售利润最大,并求最大利润.
(本小题满分12分)已知平面向量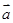
 ,
,

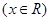 .
.
(1)若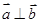 ,求
,求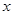 的值;
的值;
(2)若 ,求|
,求|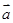 -
- |.
|.