（本小题满分12分）
已知函数f(x)＝x－ln(x＋a)．（a是常数）
(I)求函数f(x)的单调区间；
(II) 当
在x＝1处取得极值时，若关于x的方程f(x)＋2x＝x2＋b在[，2]上恰有两个不相等的实数根，求实数b的取值范围；
(III)求证:当
时
．
观察下列三角形数表：
第一行
第二行
第三行
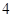
第四行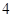
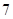
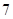
第五行
………………………………………….
假设第
行的第二个数为
.
（1）依次写出第八行的所有8个数字；
（2）归纳出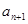
的关系式，并求出
的通项公式.
三人独立破译同一密码，已知三人各自破译出密码的概率分别为
，且他们是否译出密码互不影响。
（1）求恰有两人破译出密码的概率；
（2）“密码被破译”与“密码未被破译”的概率那个大？
用分析法证明：
.
已知
，复数
，则
（1）当
为何值时，
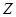为实数；
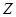（2）当为何值时，为纯虚数.
已知函数f(x)＝x－ln(x＋a)的最小值为0，其中a>0.
（1）求a的值；
（2）若对任意的x∈[0，＋∞)，有f(x)≤kx2成立，求实数k的最小值．]