已知椭圆C1的方程为
，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点。
(1) 求双曲线C2的方程；
(2) 若直线l：
与椭圆C1及双曲线C2恒有两个不同的交点，且l与C2的两个交点A和B满足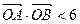
(其中O为原点)，求k的取值范围。
中心在坐标原点，焦点在x轴上的椭圆，它的离心率为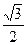
，与直线x+y－1=0相交于两点Ｍ、Ｎ，且ＯＭ⊥ＯＮ．求椭圆的方程。
椭圆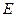
经过点
，对称轴为坐标轴，焦点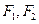
在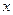
轴上，离心率
。
(Ⅰ)求椭圆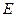的方程；
(Ⅱ)求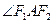
的角平分线所在直线的方程。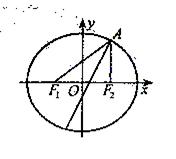
若数列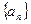
满足前n项之和
，
求：（1）bn；
(2) 
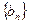的前n项和Tn。
已知数列
的首项为
=3，通项
与前n项和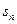
之间满足2=·
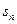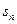
（n≥2）。
(1)求证：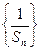
是等差数列，并求公差；
(2)求数列的通项公式。
，焦点为F，顶点为O，点P在抛物线上移动，Q是OP的中点，M是FQ的中点，求点M的轨迹方程.