(本小题满分12分)已知直线x-2y+2=0经过椭圆C: =1(
=1(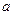 >
>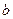 >0)的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方
>0)的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方
的动点,直线AS、BS与直线l:x=分别交于M、N两点.
(1)求椭圆C的方程;
(2)求线段MN的长度的最小值;
(3)当线段MN的长度最小时,在椭圆C上是否存在这样的点T,使得△TSB的面积为?若存在,确定点T的个数,若不存在,说明理由.
如图:在三棱锥 中,
中, 面
面 ,
, 是直角三角形,
是直角三角形, ,
, ,
, ,点
,点 分别为
分别为 的中点。
的中点。
⑴求证: ;
;
⑵求直线 与平面
与平面 所成的角的大小;
所成的角的大小;
⑶求二面角 的正切值。
的正切值。
(如图),具有公共 轴的两个直角坐标平面
轴的两个直角坐标平面 和
和 所成的二面角
所成的二面角 等于
等于 .已知
.已知 内的曲线
内的曲线 的方程是
的方程是 ,求曲线
,求曲线 在
在 内的射影的曲线方程。
内的射影的曲线方程。
如图,在三棱锥 中,
中, 底面
底面 ,
, ,
, ,
, ,点
,点 ,
, 分别在棱
分别在棱 上,且
上,且
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为
为 的中点时,求
的中点时,求 与平面
与平面 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
已知斜三棱柱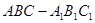 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱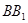 与底面
与底面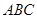 所成角为
所成角为 ,且侧面
,且侧面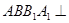 底面
底面 .
.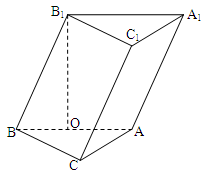
 (1)证明:点
(1)证明:点 在平面
在平面 上的射影
上的射影 为
为 的中点;
的中点;


 (2)求二面角
(2)求二面角 的大小;
的大小;
(3)求点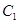 到平面
到平面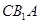 的距离.
的距离.
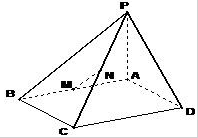
如图, 矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证:
矩形ABCD所在的平面,M,N分别为AB,PC的中点。求证: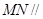 平面
平面