(12分) 阅读并解答问题
用配方法可以解一元二次方程，还可以用它来解决很多问题．例如：因为
，所以
就有最小值1，即
，只有当
时，才能得到这个式子的最小值1．同样，因为
，所以
有最大值1，即
，只有在时，才能得到这个式子的最大值1．
(1)当
= 时，代数式
有最 （填写大或小）值为 ．
(2)当= 时，代数式
有最 （填写大或小）值为 ．
(3)矩形花园的一面靠墙，另外三面的栅栏所围成的总长度是16m，当花园与墙相邻的边长为多少时，花园的面积最大？最大面积是多少?
一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同．
(1)求摸出1个球是白球的概率；
(2)摸出1个球，记下颜色后放回，并搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率(要求画树状图或列表解决)；
(3)现再将n个白球放入布袋，搅匀后，使摸出1个球是白球的概率为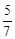
，求n的值．
如图，甲楼AB的高度为36m，自甲楼楼顶A处，测得乙楼顶端C处的仰角为45°，测得乙楼底部D处的俯角为60°，
(1)求乙楼CD的高度；
(2)从A处发现乙楼下面的店面房上的广告牌顶部E处俯角也是45°，请你确定广告牌顶部E距地面的高度是多少？(结果都保留根号)
甲、乙两校参加泰兴市科技文化中心举办的学生英语口语竞赛，两校参赛人数相等．
比赛结束后，发现学生成绩分别为7分、8分、9分、10分(满分为10分)．依据统计数据绘制了如下尚不完整的统计图表．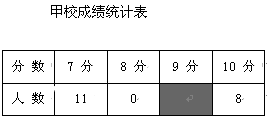
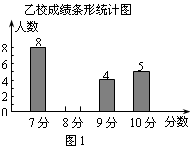
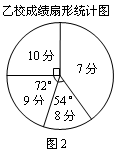
(1)请你将图1的统计图补充完整；
(2)在图2中，“7分”所在扇形的圆心角等于___________度；
(3)经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数并从平均分和中位数的角度分析哪个学校成绩较好？
(4)如果该举办单位要组织8人的代表队参加省级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析应选哪所学校？
已知：如图所示的一张矩形纸片ABCD(AD＞AB)，将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE．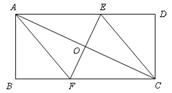
(1)求证：四边形AFCE是菱形；
(2)若AE=5cm，△CDE的周长为12cm，求矩形ABCD的面积．
已知关于x的一元二次方程x2+2(2－m)x+3－6m=0
(1)求证：无论m取什么实数，方程总有实数根；
(2)任选一个m的值，使方程的根为有理数，并求出此时方程的根．