(本题14分)如图:在二面角 中,A、B
中,A、B ,C、D
,C、D ,ABCD为矩形,
,ABCD为矩形, 且PA=AD,M、N依次是AB、PC的中点,
且PA=AD,M、N依次是AB、PC的中点,
(1)求二面角 的大小
的大小
(2)求证:
(1) 求异面直线PA和MN所成角的大小
如图,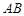 是⊙
是⊙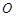 的一条切线,切点为
的一条切线,切点为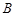 ,
,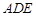 ,
,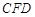 ,
,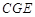 都是⊙
都是⊙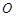 的割线,
的割线,
已知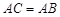 .
.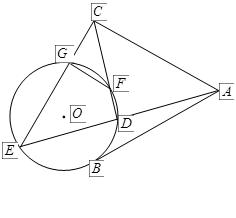
求证:
(1)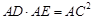 ;
;
(2)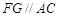 .
.
(本小题满分16分)
已知数列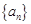 是各项均为正数的等差数列.
是各项均为正数的等差数列.
(1)若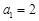 ,且
,且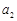 ,
,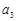 ,
,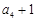 成等比数列,求数列
成等比数列,求数列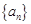 的通项公式
的通项公式 ;
;
(2)在(1)的条件下,数列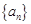 的前
的前 和为
和为 ,设
,设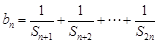 ,若对任意的
,若对任意的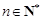 ,不等式
,不等式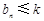 恒成立,求实数
恒成立,求实数 的最小值;
的最小值;
(3)若数列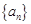 中有两项可以表示为某个整数
中有两项可以表示为某个整数 的不同次幂,求证:数列
的不同次幂,求证:数列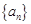 中存在无穷多项构成等比数列.
中存在无穷多项构成等比数列.
(本小题满分16分)
已知函数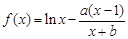 .
.
(1)当 时,若函数
时,若函数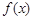 在
在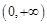 上为单调增函数,求
上为单调增函数,求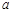 的取值范围;
的取值范围;
(2)当 且
且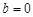 时,求证:函数f (x)存在唯一零点的充要条件是
时,求证:函数f (x)存在唯一零点的充要条件是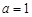 ;
;
(3)设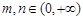 ,且
,且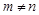 ,求证:
,求证: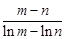 <
<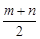 .
.
(本小题满分16分)
已知直线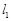 :
: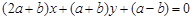 与直线
与直线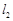 :
: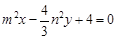 .
.
(1)当实数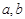 变化时,求证:直线
变化时,求证:直线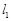 过定点,并求出这个定点的坐标;
过定点,并求出这个定点的坐标;
(2)若直线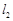 通过直线
通过直线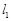 的定点,求点
的定点,求点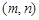 所在曲线
所在曲线 的方程;
的方程;
(3)在(2)的条件下,设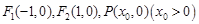 ,过点
,过点 的直线交曲线
的直线交曲线 于
于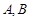 两点(
两点(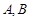 两点都在
两点都在 轴上方),且
轴上方),且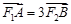 ,求此直线的方程.
,求此直线的方程.
(本小题满分14分)
某公司经销某产品,第 天
天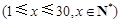 的销售价格为
的销售价格为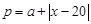 (
(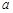 为常数)(元∕件),第
为常数)(元∕件),第 天的销售量为
天的销售量为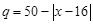 (件),且公司在第
(件),且公司在第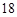 天该产品的销售收入为
天该产品的销售收入为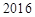 元.
元.
(1)求该公司在第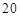 天该产品的销售收入是多少?
天该产品的销售收入是多少?
(2)这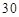 天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
天中该公司在哪一天该产品的销售收入最大?最大收入为多少?