(·湖北孝感)
2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.2-1-c-n-j-y
评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.
根据上述信息,解答下列问题:
(1)本次抽取的学生人数是 ;扇形统计图中的圆心角 等于 ;补全统计直方图;(4分=1分+1分+2分)
等于 ;补全统计直方图;(4分=1分+1分+2分)
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率. 21*cnjy*com
(·湖北襄阳,20题)为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
(·湖北武汉,19题,分)(本题8分)一个不透明的口袋中有四个完全相同的小球,它们分别标号为1,2,3,4
(1)随机摸取一个小球,直接写出“摸出的小球标号是3”的概率
(2)随机摸取一个小球然后放回,再随机摸出一个小球,直接写出下列结果:
① 两次取出的小球一个标号是1,另一个标号是2的概率
② 第一次取出标号是1的小球且第二次取出标号是2的小球的概率
(·湖北荆门,20题,分)为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.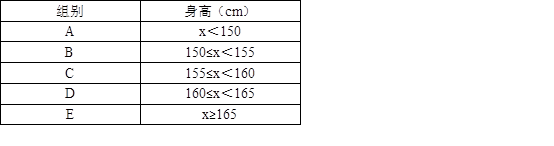
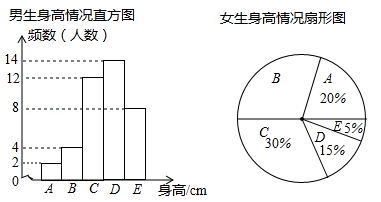
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在 组(填组别序号),女生身高在B组的人数有 人;
(2)在样本中,身高在150≤x<155之间的人数共有 人,身高人数最多的在 组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<160之间的学生约有多少人?
(·湖北黄冈,19题,分)(7 分)“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.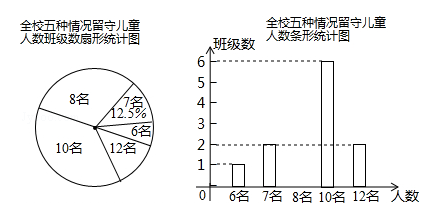
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.