(本小题满分14分)
已知数列
(1)计算x2,x3,x4的值;
(2)试比较xn与2的大小关系;
(3)设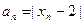 ,Sn为数列{an}前n项和,求证:当
,Sn为数列{an}前n项和,求证:当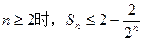 .
.
已知直线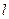 过点M(1,2),且直线
过点M(1,2),且直线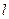 与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线
与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线 与坐标轴的交点都在正半轴上)
与坐标轴的交点都在正半轴上)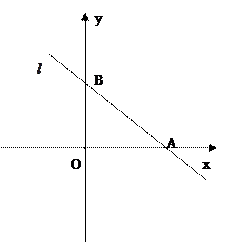 (1)若三角形AOB的面积是4,求直线
(1)若三角形AOB的面积是4,求直线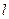 的方程。
的方程。
(2)求过点N(0,1)且与直线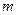 垂直的直线方程。
垂直的直线方程。
已知函数f(x)=ax3+bx2+cx是R上的奇函数,且f(1)=2,f(2)=10
(1)确定函数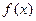 的解析式;(2)用定义证明
的解析式;(2)用定义证明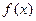 在R上是增函数;
在R上是增函数;
(3)若关于x的不等式f(x2-4)+f(kx+2k)<0在x∈(0,1)上恒成立,求k的取值范围。
)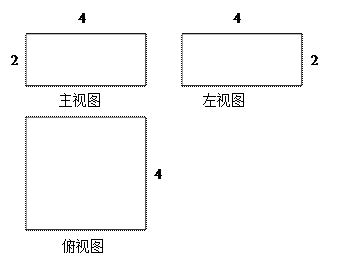 如果一个几何体的主视图与左视图都是全等的长方形,边长分别是4cm与2cm如图所示,俯视图是一个边长为4cm的正方形。
如果一个几何体的主视图与左视图都是全等的长方形,边长分别是4cm与2cm如图所示,俯视图是一个边长为4cm的正方形。
(1)求该几何体的全面积。
(2)求该几何体的外接球的体积。
某宾馆有客房300间,每间日房租为100元时,每天都客满,宾馆欲提高档次,并提高租金,如果每间日房租每增加10元,客房出租数就会减少10间,若不考虑其他因素,该宾馆将房间租金提高到多少元时,每天客房的租金总收入最高,并求出日租金的最大值?
已知函数f(x)=alnx+bx,且f(1)=-1,f′(1)=0,
⑴求f(x);
⑵求f(x)的最大值;
⑶若x>0,y>0,证明:lnx+lny≤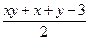 .
.