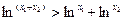从5名男生和4名女生选出4人去参加辩论比赛.
(1)求选出的4人中有1名女生的概率;
(2)设X为选出的4人中的女生人数,求X的分布列及数学期望.
二次函数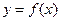 的图象经过三点
的图象经过三点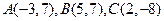 。
。
(1)求函数 的解析式;(2)求函数
的解析式;(2)求函数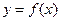 在区间
在区间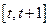 上的最大值和最小值。
上的最大值和最小值。
一辆汽车在某段路程中的行驶速度与时间的关系如下图: 
(1)求图中阴影部分的面积,并说明所求面积的实际意义;
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004k m,试将汽车行驶这段路程时汽车里程表读数S表示为时间t的函数。
m,试将汽车行驶这段路程时汽车里程表读数S表示为时间t的函数。
已知集合 。
。
(1)求
 ;(2)若
;(2)若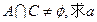 的取值范围.
的取值范围.
甲、乙等五名奥运志愿者被随机地分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者
(1)求甲、乙两人同时参加A岗位服务的概率
(2)求甲、乙两人不在同一个岗位服务的概率
(3)设随机变量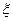 为这5名志愿者中参加A岗位服务的人数,求
为这5名志愿者中参加A岗位服务的人数,求
已知函数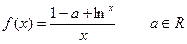
(1)求 的极值
的极值
(2)若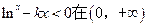 上恒成立,求
上恒成立,求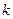 的取值范围
的取值范围
(3)已知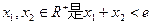 ,求证:
,求证: