已知圆M:x2+y2-4y+3=0, Q是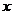 轴上的动点,QA、QB分别切圆M
轴上的动点,QA、QB分别切圆M
于A、B两点,(1)如果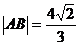 ,求点Q的坐标及直线MQ的方程;
,求点Q的坐标及直线MQ的方程;
(2)求动弦∣AB∣的最小值。
如图,在四面体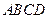 中,
中,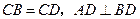 ,点
,点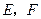 分别是
分别是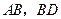 的中点.
的中点.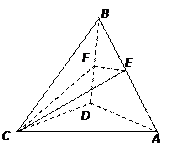
求证:(1)直线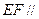 面
面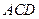 ;
;
(2)平面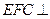 面
面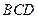 .
.
已知函数f(x)=

(1)、求f(2)与f( ),f(3)与f(
),f(3)与f( );
);
(2)、由(1)中求得结果,你能发现f(x) 与f(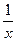 )有什么关系?并证明你的结论;
)有什么关系?并证明你的结论;
(3)、求f(1)+f(2)+f(3)+ 的值.
的值.
已知直线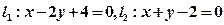 ,设其交点为点P。
,设其交点为点P。
(1)求交点P的坐标;
(2)设直线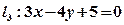 ,分别求过点P且与直线
,分别求过点P且与直线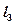 平行和垂直的直线方程.
平行和垂直的直线方程.
已知集合M={x|x2-3x+2=0},N={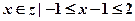 },Q={1,a2+1,a+1}
},Q={1,a2+1,a+1}
(1).求:M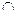 N;(2) .若M
N;(2) .若M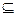 Q,求实数a的值。
Q,求实数a的值。