定义在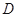 上的函数
上的函数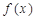 ,如果满足:对任意
,如果满足:对任意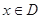 ,存在常数
,存在常数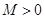 ,
,
都有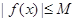 成立,则称
成立,则称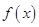 是
是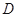 上的有界函数,其中
上的有界函数,其中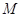 称为函数
称为函数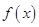 的上界.
的上界.
已知函数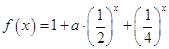 ;
; 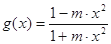
(I)当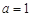 时,求函数
时,求函数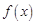 在
在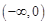 上的值域,并判断函数
上的值域,并判断函数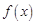 在
在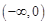 上是否为
上是否为
有界函数,请说明理由;
(Ⅱ)若函数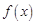 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数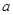 的取值范围;
的取值范围;
(Ⅲ)已知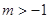 ,函数
,函数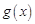 在
在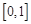 上的上界是
上的上界是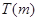 ,求
,求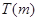 的取值范围.
的取值范围.
(本小题满分13分)已知函数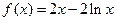

(Ⅰ)求函数在点(1, 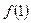 )处的切线方程
)处的切线方程
(Ⅱ)求函数 的极值
的极值
(Ⅲ)对于曲线上的不同两点 ,如果存在曲线上的点
,如果存在曲线上的点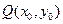 ,且
,且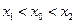 ,使得曲线在点
,使得曲线在点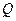 处的切线
处的切线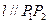 ,则称
,则称 为弦
为弦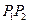 的陪伴切线.已知两点
的陪伴切线.已知两点
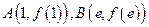 ,试求弦
,试求弦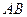 的陪伴切线
的陪伴切线 的方程;
的方程;
如图是某直三 棱柱(侧棱与底面垂直)被削去上底后的
棱柱(侧棱与底面垂直)被削去上底后的
直观图与三视图的侧视图、俯视图,在直观图中, 是
是
 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.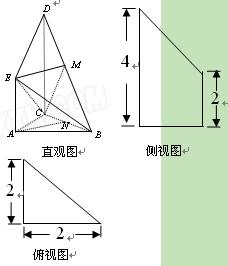
(Ⅰ)求出该 几何体的体积。
几何体的体积。
(Ⅱ)若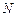 是
是
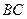 的中点,求证:
的中点,求证: 平面
平面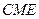 ;
;
(Ⅲ)求证:平面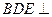 平面
平面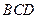 .
.
(本小题满分12分)根据市气象站 对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线
对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(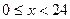 ,单位为小时,
,单位为小时,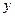 表示气温,单位为摄氏度,
表示气温,单位为摄氏度, ,
, ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整 气温最低,下午13时整气温最高。
气温最低,下午13时整气温最高。
(1)求这条曲线的函数表达式;
(2)求这一天19时整的气温。
(本小题满分12分)有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1、2、3、4.
(Ⅰ)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁 就获胜(若数字相同则为平局),求甲获胜的概率;
就获胜(若数字相同则为平局),求甲获胜的概率;
(Ⅱ)摸球方法与(Ⅰ)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
已知数列 满足
满足 =-1,
=-1, ,数列
,数列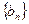 满足
满足
(1)求证:数列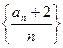 为等比数列,并求数列
为等比数列,并求数列 的通项公式.
的通项公式.
(2)求证:当 时,
时,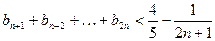
(3)设数列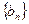 的前
的前 项和为
项和为 ,求证:当
,求证:当 时,
时, .
.