(1)计算: +(2π-1)0-
+(2π-1)0- sin45°-
sin45°- tan30°
tan30°
(2)解方程:
(3)一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1、2、3、4,小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球。
① 请你列出所有可能的结果;
② 求两次取得乒乓球的数字之积为奇数的概率。
(1)计算: .
.
(2)先化简,再求值: ,其中
,其中 .
.
已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.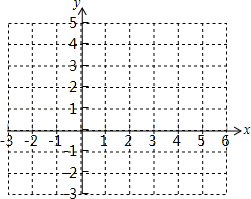
(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使得y1≥y2的x的取值范围;
(3)设抛物线与x轴的右边交点为A,过点A作x轴的垂线,交直线y2=x+1于点B,点P在抛物线上,当S△PAB≤6时,求点P的横坐标x的取值范围.
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.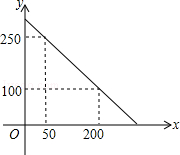
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?
如图,在直角三角形ABC中,∠ABC=90°.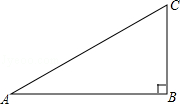
(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC=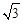 ,sinA=
,sinA=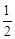 ,求△AOC的面积.
,求△AOC的面积.
某校九年级举行毕业典礼,需要从九(1)班的2名男生1名女生、九(2)的1名男生1名女生共5人中选出2名主持人.
(1)用树形图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.