如图,在平面直角坐标系中,已知点B的坐标是(-1,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,写出点P的坐标(不要求写解题过程).
阅读以下例题:“解不等式: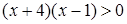
解:①当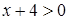 ,则
,则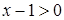 当若
当若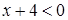 ,则
,则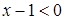
即可以写成: 即可以写成:
即可以写成:
解不等式组得: 解不等式组得:
解不等式组得:
综合以上两种情况:不等式解集: 或
或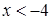
(以上解法依据:若 ,则
,则 同号)请你模仿例题的解法,解不等式:
同号)请你模仿例题的解法,解不等式:
(1) (2)
(2)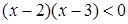
某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
| 类 别 |
电视机 |
洗衣机 |
| 进价(元/台) |
1800 |
1500 |
| 售价(元/台) |
2000 |
1600 |
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
2008年5月12日,汶川发生了里氏8.0级地震,给当地人民造成了巨大的损失.某中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:
老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:
信息一:这三个班的捐款总金额是7700元;
信息二:二班的捐款金额比三班的捐款金额多300元;
信息三:一班学生平均每人捐款的金额大于48元,小于51元.
请根据以上信息,帮助老师解决:
(1)二班与三班的捐款金额各是多少元?
(2)一班的学生人数是多少?
期中考查,信息技术课老师限时40分钟要求每位七年级学生打完一篇文章. 已知独立打完同样大小文章,小宝需要50分钟,小贝只需要30分钟. 为了完成任务,小宝打了30分钟后,请求小贝帮助合作,他能在要求的时间打完吗?
已知关于x、y的二元一次方程 的两组解是
的两组解是 和
和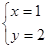
(1)求k和b的值;(2)当x=2时,求y的值。