如图1，在一个不透明的袋子中装有四个球，分别标有字母A、B、C、D，这些球除了字母外完全相同，此外，有一面白色、另一面黑色、大小相同的四张正方形卡片，每张卡片两面的字母相同，分别标有字母A、B、C、D。最初，摆成如图2的样子，A、D是黑色，B、C是白色.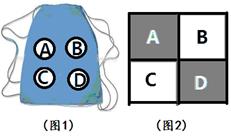
两次操作后观察卡片的颜色。
（如：第一次取出A、第二次取出B，此时卡片的颜色变成
）
（1）取四张卡片变成相同颜色的概率；
（2）求四张卡片变成两黑两白、并恰好形成各自颜色的矩形的概率.
在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．
（1）当点O为AC中点时，
①如图1，三角板的两直角边分别交AB，BC于E、F两点，连接EF，猜想线段AE、CF与EF之间存在的等量关系（无需证明）；
②如图2，三角板的两直角边分别交AB，BC延长线于E、F两点，连接EF，判断①中的猜想是否成立？若成立，请证明；若不成立，请说明理由；
（2）当点O不是AC中点时，如图3，三角板的两直角边分别交AB，BC于E、F两点，若
，求
的值．
如图，一次函数的图象与x轴，y轴分别相交于A，B两点，且与反比例函数y=
的图象在第二象限交于点C，其中点A（2，0），点B是AC的中点．
（1）求点C的坐标；
（2）求一次函数的解析式．
我校准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同，每个篮球的价格相同)，若购买3个足球和2个篮球共需310元．购买1个足球和1个篮球共需130元．求购买足球、篮球的单价各是多少元?
（1）解方程：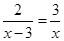 
（2）如图，AB与⊙O相切于点B，连接AO交⊙O于C，OC=BC=6，求AB.
（1）计算：
(2)已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．