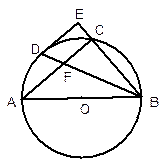如图,抛物线过点,矩形的边在线段上(点在点的左侧),点、在抛物线上,的平分线交于点,点是的中点,已知,且.
(1)求抛物线的解析式;
(2)、分别为轴,轴上的动点,顺次连接、、、构成四边形,求四边形周长的最小值;
(3)在轴下方且在抛物线上是否存在点,使中边上的高为?若存在,求出点的坐标;若不存在,请说明理由;
(4)矩形不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点、,且直线平分矩形的面积时,求抛物线平移的距离.

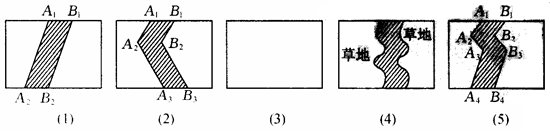
如图是图形的操作过程(四个矩形水平方向的边长均为a,竖立方向的边长均为b):将线段A1A2向右平移1个单位得到B1B2,得到封闭图形A1A2B2B1[即阴影部分如图(1)];将折线A1A2A3向右平移1个单位得到B1B2B3,得到封闭图形A1A2A3B3B2B1[即阴影部分如图(2)].
(1)在图(3)中,请你类似地画出一条有两个折点的直线,同样向右平移1个单位,从而得到1个封闭图形,并画出阴影.
(2)请你分别写出上述三个阴影部分外的面积S1=,S2=,S3=.
(3)联想与探索:如图(4),在一矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位).请你猜想空白部分草地面积是多少?
 |
如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是 否存在这样的t,使得△PMN是以PN为一直角边的
否存在这样的t,使得△PMN是以PN为一直角边的 直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.
(1)如图1,矩形ABCD中,AB=2,BC=1,请在边CD上作出A,B两点的勾股点(点C和点D除外)(要求:尺规作图,保留作图痕迹,不要求写作法);
(2)矩形ABCD中,AB=3,BC=1,直接写出边CD上A, B两点的勾股点的个数;
(3)如图2,矩形ABCD中,AB=12,BC=4,DP=4,DM=8,AN=5.过点P作直线l平行于BC,点H为M,N两点的勾股点,且点H在直线l上.求PH的长.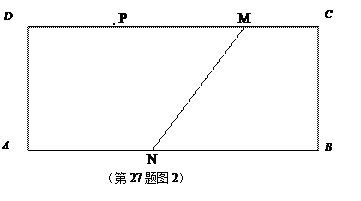
某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: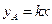 ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: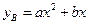 .根据公司信息部的报告,
.根据公司信息部的报告,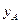 ,
,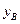 (万元)与投资金额
(万元)与投资金额 (万元)的部分对应值如下表所示:
(万元)的部分对应值如下表所示:
 |
1 |
5 |
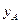 |
0.8 |
4 |
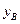 |
3.8 |
15 |
(1)填空: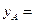 ;
;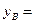 ;
;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为w(万元),试写出w与某种产品的投资金额x之间的函数关系式;
(3)请你设计一个在⑵中能获得最大利润的投资方案.
如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F.⑴求证:DE是⊙O的切线;(2) 若CE=1,ED=2,求⊙O的半径.