下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°
∴∠AOC=55°
若你是老师,会判小马虎满分吗?
若会,说明理由.
若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
表1.
| 1 |
2 |
3 |
﹣7 |
| ﹣2 |
﹣1 |
0 |
1 |
(2)数表A如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值
表2.
| a |
a2﹣1 |
﹣a |
﹣a2 |
| 2﹣a |
1﹣a2 |
a﹣2 |
a2 |
某地计划用120﹣180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石比原计划多5000米3,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.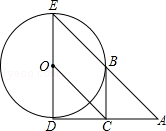
(1)求AD的长;
(2)BC是⊙O的切线吗?若是,给出证明;若不是,说明理由.
某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
| 分组 |
划记 |
频数 |
| 2.0<x≤3.5 |
正正 |
11 |
| 3.5<x≤5.0 |
 |
19 |
| 5.0<x≤6.5 |
||
| 6.5<x≤8.0 |
||
| 8.0<x≤9.5 |
 |
2 |
| 合计 |
50 |
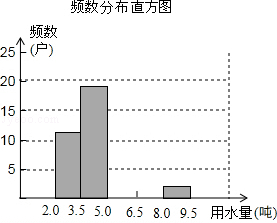
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
先化简,再求值: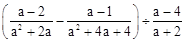 ,其中
,其中 .
.