(本小题满分12分)
设函数
(Ⅰ)若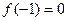 且对任意实数
且对任意实数 均有
均有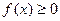 成立,求
成立,求 表达式;
表达式;
(Ⅱ)在(Ⅰ)的条件下,当 时,
时,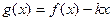 是单调函数,
是单调函数,
求实数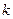 的取值范围;
的取值范围;
(Ⅲ)设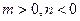 ,且
,且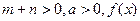 为偶函数,求证
为偶函数,求证
如图,圆台上底半径为1,下底半径为4,母线AB=18,从AB中点M拉一条绳子绕圆台侧面转到A点。
(1)求绳子的最短长度;
(2)求绳子最短时,上底圆周上的点到绳子的最短距离。
如图2-72,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是B1C1、C1D1的中点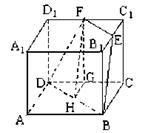
(1)求证:E、F、B、D四点共面;
(2)求四边形EFDB的面积.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.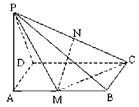
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
如图所示,已知空间四边形ABCD,E、F分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且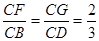 ,求证直线EF、GH、AC交于一点.
,求证直线EF、GH、AC交于一点.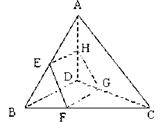
如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB、BC的中点,G为DD1上一点,且D1G:GD=1:2,AC∩BD=O,求证:平面AGO//平面D1EF.